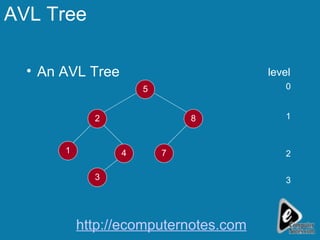
The document discusses various aspects of balanced binary search trees, including: 1) Const keyword can be used to mark parameters and return values as constant to prevent unintended modification. 2) AVL trees are binary search trees where the heights of left and right subtrees differ by at most 1. 3) For a binary search tree to be balanced, the heights of left and right subtrees should be close to equal to avoid a skewed or degenerate tree structure.

1. Class No.19 Data Structures http://ecomputernotes.com

2. The const Keyword The answer is that, yes, we don’t want the function to change the parameter, but neither do we want to use up time and memory creating and storing an entire copy of it. So, we make the original object available to the called function by using pass-by-reference. We also mark it constant so that the function will not alter it, even by mistake. http://ecomputernotes.com

3. The const Keyword Use 2 : The const keyword appears at the end of class member’s function signature: EType& findMin( ) const; Such a function cannot change or write to member variables of that class. This type of usage often appears in functions that are suppose to read and return member variables. http://ecomputernotes.com

4. The const Keyword Use 3 : The const keyword appears at the beginning of the return type in function signature: const EType& findMin( ) const; Means, whatever is returned is constant. The purpose is typically to protect a reference variable. This also avoids returning a copy of an object. http://ecomputernotes.com

5. Degenerate Binary Search Tree BST for 14, 15, 4, 9, 7, 18, 3, 5, 16, 20, 17 14 15 4 9 7 18 3 5 16 20 17 http://ecomputernotes.com

6. Degenerate Binary Search Tree BST for 3 4 5 7 9 14 15 16 17 18 20 14 15 4 9 7 18 3 5 16 20 17 http://ecomputernotes.com

7. Degenerate Binary Search Tree BST for 3 4 5 7 9 14 15 16 17 18 20 14 15 4 9 7 18 3 5 16 20 17 Linked List! http://ecomputernotes.com

8. Balanced BST We should keep the tree balanced . One idea would be to have the left and right subtrees have the same height http://ecomputernotes.com

9. Balanced BST Does not force the tree to be shallow . 14 15 18 16 20 17 4 9 7 3 5 http://ecomputernotes.com

10. Balanced BST We could insist that every node must have left and right subtrees of same height. But this requires that the tree be a complete binary tree To do this, there must have (2 d+1 – 1 ) data items, where d is the depth of the tree. This is too rigid a condition. http://ecomputernotes.com

11. AVL Tree AVL (Adelson-Velskii and Landis) tree. An AVL tree is identical to a BST except height of the left and right subtrees can differ by at most 1. height of an empty tree is defined to be (–1). http://ecomputernotes.com

12. AVL Tree An AVL Tree 5 8 2 4 3 1 7 level 0 1 2 3 http://ecomputernotes.com

13. AVL Tree Not an AVL tree 6 8 1 4 3 1 5 level 0 1 2 3 http://ecomputernotes.com

14. Balanced Binary Tree The height of a binary tree is the maximum level of its leaves (also called the depth). The balance of a node in a binary tree is defined as the height of its left subtree minus height of its right subtree. Here, for example, is a balanced tree. Each node has an indicated balance of 1, 0, or –1. http://ecomputernotes.com

15. Balanced Binary Tree -1 0 1 0 0 0 0 -1 0 1 0 0 0 0 0 0 0 http://ecomputernotes.com